

#Matlab norm code#
#Matlab norm download#
(Converegnce Analysis of SL0): Hossein Mohimani, Massoud Babaie-Zadeh, Irina Gorodnitsky, Christian Jutten, "Sparse Recovery using Smoothed L0 (SL0): Convergence Analysis" submitted (on 24 January 2010) to IEEE Transactions on Information Theorey ( Download it from arXiv)."Complex-Valued Sparse Representation Based on Smoothed L0 Norm" in proceedings of ICASSP2008, Las Vegas, April 2008, pp. Hossein Mohimani, Massoud Babaie-Zadeh, Christian Jutten,.Hossein Mohimani, Massoud Babaie-Zadeh, Christian Jutten, "A fast approach for overcomplete sparse decomposition based on smoothed L0 norm", IEEE Transactions on Signal Processing, Vol.57, No.1, January 2009, pp.Hossein Mohimani, Massoud Babaie-Zadeh, Christian Jutten, "Fast Sparse Representation based on Smoothed L0 norm", in proceedings of 7th International Conference on Independent Component Analysis and Signal Separation (ICA2007), LNCS 4666, September 2007, London, pp.The first paper was titled "Fast Sparse Representation based on Smoothed L0 norm", and had been submitted to IEEE Signal Processing letters on.Since the value of &sigma has only slightly decreased, we hope that the minimizer of F &sigma(.) for this new &sigma is not too far from the minimizer of F &sigma(.) for the previous (larger) &sigma, and hence we hope to not get trapped into a local minima. The minimum of F &sigma(.) is used as a starting point to locate the minimum of F &sigma(.) for the next (smaller) &sigma, using a steepest descent approach.

Then, the idea of SL0 for escaping from these local minima is to use a "Gratuated Non-Convexity (GNC)" procedure: It starts with a very large &sigma (for which there is no local minima), and decreases gradually &sigma to zero. However, this is difficult, because for small values of &sigma, F &sigma(.) is highly non-smooth with a lot of local minima. The goal is then to minimize F &sigma( s) for a very small value of &sigma. Moreover, for &sigma &rarr &infin, F &sigma(.) tends to a very smooth and convex function (contrary to the L0 norm itself).
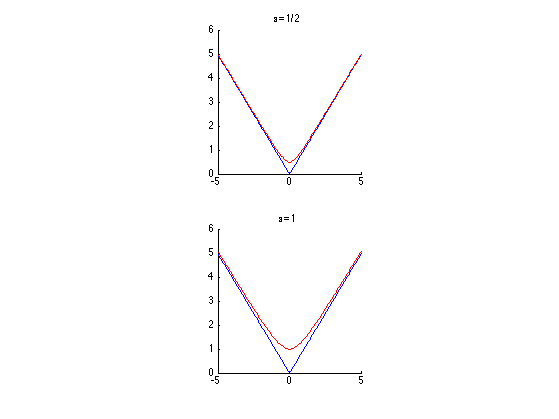
The approximation tends to equality for &sigma &rarr 0. More precisely, it approximates the L0 norm of a vector s by a smooth function F &sigma( s), where &sigma determines the quality of approximation: The larger &sigma, the smoother F &sigma(.) but worse approximation to the L0 norm and the smaller &sigma, the better approximation to the L0 norm but the less smooth F &sigma(.). The main idea of SL0 is to use a "smooth" measure of the L0 norm. Note also that the equivalence of minimizing L1 and L0 is only assymptotic, and does not always hold (for a counter-example, see here). Basis Pursuit), which replace L0 norm by other cost functions (like L1). This is contrary to most of other existing algorithms (e.g.


 0 kommentar(er)
0 kommentar(er)
